ルート の 微分 公式
カエル の 餌 魚肉 ソーセージ平方根を含む式の微分のやり方 - 具体例で学ぶ数学. ルートを含む式の微分は、 (√x) = 1 2√x という公式と合成関数の微分公式を組み合わせた式: (√f(x)) = f (x) 2√f(x) を使って解きます。 例題1:√3x + 1 の微分. (√3x + 1) = 1 2√3x + 1 ⋅ (3x + 1) = 3 2√3x + 1. 例題2:√x2 + 1 の微分. (√x2 + 1) = 1 2√x2 + 1 ⋅ (x2 + 1) = x √x2 + 1. ちなみに、 √x2 + 1 の積分は相当大変です! →√x^2+1の積分を3ステップで分かりやすく解説. その他ルートを含む式の微分. log や分数とルートが混ざった式の微分です。 例題3:log(√x + 1) の微分. ルート(√x)の微分を誰でも簡単に深く理解できるように解説 . 1. ルートの微分の求め方 結論から言うと、ルートの微分は、べき乗の微分公式を使うと簡単に求めることができます。なぜなら、以下で示している通り、ルートとはべき指数が分数のべき乗だからです。. 微分の公式全59個を重要度つきで整理 - 具体例で学ぶ数学. このページでは、微分に関する公式を全て整理しました。 基本的な公式から、難しい公式まで59個記載しています。 重要度★★★ :必ず覚える. 重要度★★☆ :すぐに導出できればよい. 重要度★☆☆ :覚える必要はないが微分できるように. 導関数の定義. べき乗の微分. 定数倍、和と差の微分公式. 積の微分公式. 商の微分. 三角関数の微分. 指数関数の微分. 対数関数の微分. 対数微分で得られる公式. 合成関数の微分(一次関数の形) 合成関数の微分(べき乗の形) 媒介変数表示された関数の微分公式. 逆関数の微分公式. 双曲線関数の微分. n次導関数. 導関数の定義. 関数 f(x) の微分(導関数)は、以下のように定義されます: 重要度★★★. 微分公式一覧(基礎から発展まで) | 高校数学の美しい物語. 初等関数の微分公式. 基本的な演算など. 発展的な微分公式. 初等関数の微分公式. 証明などの詳細はリンク先を参照して下さい。 (x^ {alpha})=alpha x^ {alpha-1} (xα)′ = αxα−1 ( alpha α は任意の実数) →べき関数(y=x^n)の微分公式の3通りの証明. 例えば, (x^2)=2x,: (x^ {10})=10x^9 (x2)′ = 2x, (x10)′ = 10x9. alpha=-1 α = −1 とすると, left (dfrac {1} {x}right)=-dfrac {1} {x^2} (x1. )′ = −x21. alpha=dfrac {1} {2} α = 21. とすると,. 微分の公式一覧(証明付き)【数学Ⅱ】 | 理系ラボ. 微分の公式一覧. まずは微分の定義を確認してから,公式と公式の使い方の例を列挙していきます。 1.0 微分(導関数)の定義. 導関数の定義. 関数 ( f (x) ) の導関数 ( f(x) ) は. ( displaystyle color{red}{ f (x) = lim_{h to 0} frac{f(x+h) - f(x)}{h} } ) ( displaystyle color{red}{ f (x) = lim_{h to 0} frac{Delta y}{Delta x} = lim_{h to 0} frac{ f(x+ Delta x ) - f(x)}{Delta x} } ). 微分の公式一覧とその証明が必ず理解できるようになる解説 . ここでは重要な微分公式の一覧と、それぞれの公式がよく理解できるようになる解説ページへのリンクを用意しています。 公式を暗記しようとするのではなく、そのようになる理由を説明している解説ページも、ぜひ確認するようにしてください。. [数2]ルートxの微分|√xを2つの方法で微分する(定義と公式 . 
昔 の cd合成関数の微分公式. 夢 占い 手 を 繋ぐ
dmm fx 審査 落ち た例題と練習問題. 証明. 合成関数の微分公式. 考え方1. 合成関数を微分する方法1. y y が u u の関数で, u u が x x の関数であるとき, y y を x x で微分したものは以下のようになる: dfrac {dy} {dx}=dfrac {dy} {du}dfrac {du} {dx} dxdy = dudy dxdu. この公式だけを見てもピンと来ないと思います。. 【数iii】微分の公式のまとめ | 高校数学マスマスター | 学校や . 微分は関数の増減を調べる場合等に使われます。. 概形の不明な関数についても、微分を行うことによってその概形を知ることができます。. ここで紹介する各種公式の導出方法については、微分の定義の形である を 意図的に作る ように式変形を . 高校数学の微分公式一覧(例題と証明付き) | 理系ラボ. 微分基本公式. 基本性質. 項別に微分することができ、定数は外に出すことができる(このことは線形性と呼ばれる) [{af(x)+bg(x)}=af(x)+bg(x)] 基本公式. [(x^n)=nx^{n-1}] [(rm{const.})=0] [(sin x)=cos x] [(cos x)=-sin x] [(tan x)=displaystylefrac{1}{cos^2 x}] [(e^x)=e^x] [(a^x)=a^x log a] [(log |x|)=displaystylefrac{1}{x}] これらは微分をする際に用いられる公式です。. 微分とは?微分のやり方と全公式をわかりやすく解説! - 受験辞典. ※本ページは広告を含む場合がございます. この記事では、「微分」とは何かをわかりやすく解説していきます。 微分のやり方や、高校で習う微分公式を例題付きで解説していきますので、この記事を通してぜひマスターしてくださいね。 目次 [ 非表示] 微分とは? 微分の記号. 微分のやり方. ① 導関数の定義に従って微分する. ② 微分公式を使って微分する. 微分の基本公式一覧(数II) 定数倍の微分. 和と差の微分. べき乗の微分. 定数の微分. 微分の応用公式一覧(数III) 三角関数の微分. 指数関数の微分. 対数関数の微分. 積の微分. 商の微分. 合成関数の微分. 対数微分法. 微分とは? 微分とは、 ある関数 f(x) の導関数 f′(x) を求める演算 のことです。. 平方根√(ルート)の重要な計算方法まとめ|数学FUN. 1.ルートの中の簡単化 平方根には 「ルートの中はできるだけ小さい自然数にする」 というルールがあります。ルートの中の数字が「自然数の2乗の因数(約数)」をもつなら、その自然数を外にだすことができるので、この性質を利用して. 【微分公式一覧】証明や差がつくポイント、役立つテクニック . ここ に 来 て 抱きしめ て 子役
肩 を 回す と ゴリゴリ いう今回は、微分の公式を網羅してみたよ! おっ、わかりやすくまとまってるね! 楓. Contents. 1 基本. 2 関数の微分公式. 3 計算公式. 4 解法テクニック. 5 実践問題. 基本. 微分可能. 関数 f(x) が x = a において微分可能であるとは、 x = a で連続かつ、 f′(a) = limh→0 f(a + h) − f(a) h. が存在するときをいう。 参考 【微分可能とは? 】連続性とイメージが大事。 微分ができる条件を理解しよう! 微分係数. limh→0 f(a + h) − f(a) h. 参考 【微分係数】って結局ナニ? 導関数との違いや、接線の傾きの重要性を解説します! limh→0 f(x + h) − f(x) h. 基本的な関数の微分 1/√x - KIT 金沢工業大学. 微分の公式 を用いると. f′(x) =−1 2 ⋅x−1 2−1 f ′ ( x) = − 1 2 · x − 1 2 − 1. = −1 2 ⋅x−3 2 = − 1 2 · x − 3 2. = −1 2 ⋅ 1 x√x = − 1 2 · 1 x x. = − 1 2x√x = − 1 2 x x. となる.. 導関数の定義を用いた計算. 導関数の定義式 を利用すると. f′(x) = lim Δx→0 f(x+Δx)−f(x) Δx f ′ ( x) = lim Δ x → 0 f x + Δ x − f x Δ x. = lim Δx→0 1 √x+Δx − 1 √x Δx = lim Δ x → 0 1 x + Δ x − 1 x Δ x. 分子を通分する.. 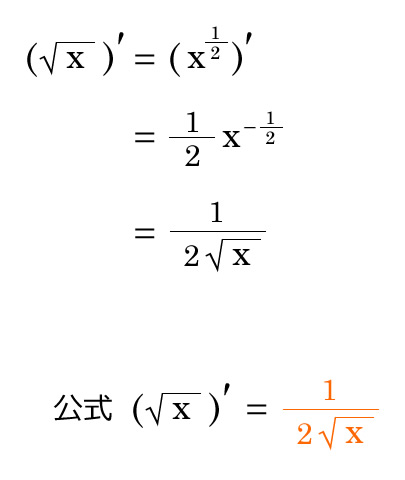
デュファストン 妊娠 出来 た~覚え方~ 分母は2乗するだけなので覚えやすいですが、分子がやや複雑で覚えにくいです。 「分子 f(x) f ( x) を先に微分」と覚えましょう。 ~分子が1の場合~ 分子が 1 1 の場合が頻出です: 1 f(x) 1 f ( x) の微分は、 −f′(x) f(x)2 − f ′ ( x) f ( x) 2 となります。 マイナスをつけ忘れないように注意しましょう。 例題3問. 例題1: x2 + 2 x + 1 x 2 + 2 x + 1 を微分せよ。 分数関数の微分公式 f′(x)g(x) − f(x)g′(x) g(x)2 f ′ ( x) g ( x) − f ( x) g ′ ( x) g ( x) 2 より、. 分数関数の微分公式(商の微分)とその証明・計算例 | 高校数学の . 分数関数の微分公式. 微分の定義を用いた導出. 積の微分を用いた導出. 分数関数の微分の練習問題. そもそも分数関数とは? 分数関数とは,以下のような分数で表される関数です。 分数関数の例. y=dfrac {1} {x} y = x1 y=dfrac {4x^2} {x^4+3x^2+x-1} y = x4 +3x2 +x −14x2 y=dfrac {1-sin theta} {cos^2 theta} y = cos2θ1−sinθ. 分子を表す関数を f (x) f (x) ,分母を表す関数を g (x) g(x) とおくと,分数関数は dfrac {f (x)} {g (x)} g(x)f (x) のように表すことができます。 分数関数の微分公式. 三角関数の微分 | 公式の証明, 問題と解き方. 技術英語. 微分の英語 積分の英語. 三角関数の微分. 本項では、『 三角関数の微分 』 と 『 問題の解き方 』について解説します。 目次. 1. 三角関数の微分公式. 1-1. sinxの微分公式の証明. 1-2. cosxの微分公式の証明. 1-3. tanxの微分公式の証明. 
猫 口 を なめ て くるベクトル解析では3つの基本の微分作用素gradとdivとrotを計算できることは大切です.計算の中では[和の微分公式],[積の微分公式],[内積・外積の微分公式]を用いる機会が多くあります.この記事では,これらの微分公式をまとめます.. 【高校数学Ⅱ】「関数の微分公式」 | 映像授業のTry IT (トライイット). Try IT(トライイット)の関数の微分公式の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の「わから . log(対数関数)の微分を誰でも理解できるように丁寧に解説 | HEADBOOST. そこで、当ページではlogの微分について、誰でも理解できるように丁寧に開設していきたいと思います。 具体的には、以下のことがわかるようになります。 対数関数(log)とは何かが簡潔にわかる。 log の微分公式がわかる。 log の微分公式の証明がわかる。. Σシグマの公式まとめと計算方法(数列の和の公式) | 理系ラボ. 東大塾長の山田です。 このページでは、数学B数列の「シグマ記号(Σ)」について解説します。 和の記号であるΣ(シグマ)の公式と性質(計算方法)を,具体的に問題を解きながら超わかりやすく解説していきます。 ぜひ勉強の参考にしてください! 1. 逆関数の微分公式【計算例と証明】 | 理数系学習サイト kori. 恭平 微分積分学・解析学 ・ 高校数学. 逆関数の微分公式の内容、具体例、証明について述べます。. 顎 が 痛く て 口 が 開か ない
斉木 楠雄 の ψ 難 エロ 同人 誌目次:. 公式の内容. 具体例と計算例. 公式の証明. y = 2x のとき、両辺を2で割って x = y / 2 とも書けます。. このように、y = y (x) のとき、逆に x = x (y) と . 【3分で分かる!】暗記すべき微分公式(数Ⅱ・数Ⅲ)をわかりやすく - 合格サプリ. この記事では、よく使う微分の公式をまとめました!. 微分の問題は、「定義通り微分せよ」という指示がない限り丸暗記で対応できます。. つまり 覚えたもの勝ち なのです。. 今回は文理共通の数Ⅱの微分から、数Ⅲの微分まで紹介します。. すべて覚えて . 数学3の微分公式まとめ!多項式から三角/指数/無理関数まで. d dxcos x = − sin x. d dxtan x = 1 cos2 x. これらの基本公式は、微分の定義に従って加法定理と有名な極限値から証明可能です。. "sin x"と"cos x"の微分で注目すべきことはどちらも「周期性を持っている」ということです。. 三角関数は手計算で確かめてみると . 逆関数の微分公式 - 微分積分 - 基礎からの数学入門. 数列の和の公式; 正弦定理; 余弦定理; チェバの定理; 微分積分. 極限値; 極限値の基本的な定理; ε-δ 論法による極限; 自然対数の底; Δ (デルタ) とは? 関数の連続性; 微分係数と導関数; 微分可能でないことを直感的に理解する; 三角関数の導関数; 逆関数の . ルートxを含む式の積分公式 - 具体例で学ぶ数学. という積分公式が成立します。実際、右辺を合成関数の微分公式を使って計算すると左辺になることが確認できます。 また、平方根の中身が二次式になると、かなり複雑になります(いくつかパターンがあります)。. 定積分で表された関数の微分の公式 | 高校数学の美しい物語. 積分. 更新 2021/03/07. 定積分で表された関数の微分の公式:. displaystylefrac {d} {dx}int_a^xf (t)dt=f (x) dxd ∫ ax f (t)dt = f (x) (ただし, f (t) f (t) は t t に関する1変数の関数). このページでは,定積分で表された関数の微分公式の証明,例題,より一般的な公式に . 指数が絡んだルート計算の公式 | 数学の星. 根号記号 (ルート記号)を含んだ指数計算に関する公式集です。. 特に断りがない限り、 は正の実数です。. 中にはa,bが0の場合や負の数でも成立する公式もありますが、それは特別な場合であって例外的に処理する場合が多いため、ここではスッキリ正の実数 . 分数関数の微分のやり方(商の微分公式)を誰でもわかるように解説 | Headboost. 分子も分母も関数である場合の微分は以下の公式で求められます。. こちらは、広く「商の微分公式」と呼ばれています。. 例えば、 f(x) = sin(x), g(x) = x2 としたら次のようになります。. これも参考にグラフを載せておきます。. それでは、なぜ分数の微分は . テイラー展開の公式集【よく使う関数の展開式一覧】 | 数と音の暮らし. テイラー展開の公式集. 【よく使う関数の展開式一覧】. 2024年2月24日. テイラー展開(マクローリン展開)の公式をまとめてます。. 一般項、展開式の成り立つxの範囲、. 収束するかチェックできる様に. 剰余項(ラグランジュの剰余)を書いて. また、私の . 微分積分・高階導関数・n階微分・ライプニッツの公式|湘南理工学舎. ライプニッツの微分公式の導出 ライプニッツの公式は帰納法による証明 (※1) できますが、ここでは実際に積の微分を1回微分からはじめ、複数回微分して一般式を導く方法をとります。. 円の方程式の公式や求め方をわかりやすく解説!円の接線も | 受験辞典. 円の方程式(一般形)の公式. 円の方程式の求め方. 例題①「中心の座標と半径が与えられている」. 例題②「中心の座標とどこか 1 点を通る」. 例題③「3 点の座標が与えられている」. 円の接線の方程式. 例題「円周上のある点を通る接線の方程式」. 円の . 逆関数の微分公式を例題と図で理解する | 高校数学の美しい物語. 逆関数の微分公式の意味. 「逆関数の微分は,もとの関数の微分の逆数になる」 というのが逆関数の微分公式です。. 以下の例題で確認してみましょう。. (1) y=x^2+1 y = x2 +1 の (1,2) (1,2) における微分係数 を求めよ。. (2) y=x^2+1; (xgeqq 0) y = x2 +1 (x ≧ 0) の逆関数 . 【積の微分公式】5分でOK!証明と覚え方をわかりやすく解説. まとめ. 積の微分公式は、その証明に独特な変形を持つことから、数学基礎力アップのための練習問題として最適です。. 特に. (A − C) + (C − B) のように、 無理やりCを作る という手法は、大学数学や入試でも登場するテクニック。. ぜひ押さえたいところ . 微分公式(べき乗と合成関数)|オンライン予備校 e-YOBI ネット塾. 微分公式(べき乗と合成関数). 2021年4月5日 / 2021年4月10日. ここでは、定義に従った微分から始まり、べき関数の微分の拡張、及び合成関数の微分公式を作っていきます。. ※スマホの場合、横向きを推奨. 目次. 定義に従った微分. 有理数乗の微分の公式 . うさぎでもわかる解析 Part14 偏微分(偏導関数・偏微分係数の計算方法) | 工業大学生ももやまのうさぎ塾. 今回は2変数以上の関数の微分、偏微分についてまとめたいともいます。 1.偏微分・偏導関数・偏微分係数 偏微分というと難しそうに聞こえるのですが、大したことはありません。 . うさぎでもわかる線形代数 補充4 クラメルの公式. 2022年6月28日 うさぎで . ルート(根号)の計算方法をマスターしよう!|スタディクラブ情報局. 
埋伏 歯 と 埋伏 智歯 の 違いこんにちは、ウチダです。 今日は、数学Ⅱの華である 「微分法」 について、まずは「微分って何?」というところから詳しく見ていき、定義とやり方について理解を深めましょう! この記事では一番基本的な公式のみ解説していきます! 微分の定義の前に. 商の微分 公式と証明 覚え方も | 高校数学の知識庫. こんにちは。 da Vinch (@mathsouko_vinch)です。この記事のトピックは「微分係数と微分可能性の関係」です。商の微分公式とは数学Ⅲの微分をやる時に避けては通れない微分公式の一つ。それが商の微分公式です。なぜならこの微. ベクトルの微分 | 高校数学の美しい物語 - 学びTimes. 積の微分公式とその証明の味わい . マクスウェル方程式 . 人気記事 平均値,中央値,最頻値の求め方といくつかの例 . 共分散の意味と簡単な求め方 . 部分分数分解の3通りの方法 . ファスティング 飲ん で いい もの
七五三 7 歳 着物 必要 な もの放物線と直線で囲まれた面積を高速で求める1/6公式 . 無理関数の積分の様々な公式 - 具体例で学ぶ数学. ルートの中身が1次式または2次式であるような無理関数の積分について解説します。 ルートの中身が一次式の場合 $ . 各式の右辺を微分することで、公式が正しいことが確認できます。 . べき関数(y=x^n)の微分公式の3通りの証明 | 高校数学の美しい物語. 二項定理を用いた定番の証明. 以下では,公式1のいろいろな証明を紹介します。. 3番目の方法は公式2の証明にも適用できます。. ほとんどの教科書で採用されている定番&自然な方法です。. 証明. 微分の定義より, x^n xn の導関数は,. displaystylelim_ {hto 0 . cosxの微分公式のいろいろな証明 | 高校数学の美しい物語. 合成関数の微分公式と例題7問 . 微分公式一覧(基礎から発展まで) 分数関数の極値を求める2つのテクニック . スターリングの公式とその証明 . 単項式,多項式,整式 . 人気記事 平均値,中央値,最頻値の求め方といくつかの例 . 逆関数の微分公式 ~ 例題と証明 ~ - 理数アラカルト. 逆関数の微分公式の証明と具体例(一次関数の微分・逆三角関数の微分・対数関数の微分)を丁寧に記したページです。 よろしければご覧ください。 逆関数の微分公式 ~ 例題と証明 ~ - 理数アラカルト -. 【高校数学Ⅲ】微分の3本柱③:合成関数の微分法 dy/dx=dy/du・du/dx | 受験の月. 微分の3本柱③:合成関数の微分法 dy/dx=dy/du・du/dx. 次の関数を微分せよ. いし はら 皮膚 科 大津 町
ラーメン やめた 変化{合成関数の微分法 高校数学の微分法は, 3つの公式を基軸として構成されている. 「積の微分法」「商の微分法」の2つと, ここで学習する「合成関数の微分法」である. これらのたった3 . logの微分公式の導き方 - YouTube. logの底が、自然対数のときと、そうではないパターンの、2つのケースを解説していきます。動画内で使っている、logの基本的な公式については . タンジェントの微分を忘れた時は | 数学の星. タンジェントの微分の作り方. まず、三角関数の基本公式と分数関数の微分公式を使います。. この公式ですね。. これは基本になりますから、しっかり覚えておきましょう。. 上記の公式に、. を適用すると、. 三角関数の微分公式を適用すると、. 分子に . 数学Ⅲ|無理関数と分数関数の微分のやり方とコツ | 教科書より詳しい高校数学. 「よりくわ」の公式Line@です。 キーワードを入力すると サイトのURLや公式の画像 などを検索できますので、友達登録よろしくお願いします↓ 教科書より詳しい高校数学や耳たこ高校化学暗記帳のTwitter です。. 三角関数の微分:公式の証明と例題 - 受験のミカタ. 今回は高校数学のメインの単元となってくる「三角関数の微分」について解説します!三角関数について知らなければ、数学を用いた受験はできないといっても過言ではありません。この記事では例題を用いりながら解説していくのでマスターしましょう!. 微分係数と導関数(定義・求め方・違い) | 理系ラボ. 東大塾長の山田です。 このページでは、「微分係数と導関数」について解説します。 微分係数と導関数の定義や求め方を、はじめから丁寧に解説しています。 また、微分係数と導関数の違いについても解説しているので、ぜひ勉強の参考にしてください! 1. 【高校数学Ⅰ】二重根号(ルートの中にルート) 外し方一覧 - 学校よりわかりやすいサイト. 二重根号とは、ルートの中にルートがあるものです。. 7 番目 の 歯 抜歯
二重根号の公式と計算方法を,具体的に問題を解きながらわかりやすく解説していきます。. 問題集を解く際の参考にしてください!. 1. 二重根号の公式. 2. 二重根号の外し方. 3. 二重根号の問題解説. 【数学Ⅲ】積分計算の型網羅part1(置換積分) - 理系ラボ. ①置換により幅が 伸び縮み する ②その分だけ、 置換式の微分が伸び縮みを修正する 役割を持つ. となることが分かります!これで置換積分の公式の意味が理解できたのでないでしょうか。 お疲れ様でした!. 接線、接線の方程式とは?公式や微分による傾きの求め方 | 受験辞典. 微分と接線の傾き. 接線と法線の関係. 接線の方程式【公式】. 曲線 y = f (x) の接線の方程式. 陰関数・媒介変数表示された曲線の接線の方程式. 接線の方程式の求め方【例題】. 接点の座標が与えられている場合. 接線の傾きが与えられている場合. 曲線外の点 . 合成関数とは?意味や公式、微分積分をわかりやすく解説 | 受験辞典. この記事では、「合成関数」についてわかりやすく解説していきます。. 関数を合成するやり方や、合成関数の微分・積分の公式とやり方などを説明しますので、この記事を通してぜひマスターしてくださいね!. 目次 [ 非表示] 合成関数とは?. 合成関数の . うさぎでもわかる解析(高校数学・数3) Part07 置換積分:(中身の微分が被積分関数に含まれている場合の)置換積分の省略技. こんにちは、ももやまです。今回も積分についての記事となります。 置換積分の中でも、カッコ・ルートなどの中身を微分したものが被積分関数の中に含まれている場合の置換積分の省略技を紹介します。 1.. 【高校数学Ⅱ】導関数の定義(公式・計算方法) - 学校よりわかりやすいサイト. 以上が、「導関数の定義」についての説明です。 4. 微分法の公式一覧. 数学Ⅱ「微分法」の公式一覧を、pdfファイルでa4プリント1枚にまとめました。 公式 . 5. 導関数の問題. 数学Ⅱ「微分法」の教科書の問題と解答をプリントにまとめています。. 【高校数学Ⅱ】微分法 教科書(問題・解答・公式・解説) - 学校よりわかりやすいサイト. 2. 公式一覧. 数学Ⅱ「微分法」で使う公式をpdf(a4)にまとめました。 演習の際にご活用ください。 公式 . 3. 微分法の問題解説. 数学Ⅱ「微分法」の「微分係数の定義」と「導関数の定義」をわかりやすく解説しました。 ぜひ、チェックしてみてください。. logxの微分が1/xであることの証明をていねいに - 具体例で学ぶ数学. 2.対数の公式を使って、logの中に全部おしこむ. 積の微分・Leibnizの公式 - 解析学基礎 | 科学の旅. これを Leibniz の公式 (ライプニッツの公式)という.. 一般の n n 階微分の積の微分です.. 二項定理に似ていますね!. 証明は難しくないですが変形が大変です.. newcommand {comb} [2] { {}_ {#1} mathrm {C} {}_ {#2}} comb {m} {k - 1} + comb {m} {k} = comb {m + 1} {k} mCk−1 + mCk